PROOF OF ICOSAHEDRAL CENTRE
Lemma 1
The 2 diagonals of a regular pentagon intersect
each other in the ratio Ø : 1, where Ø is the golden mean defines as follows. Take a line AB and a point C on
it. Then, if AB:AC = AC:CB we say that C divides AB
in the golden ratio, and that each of the above ratios is
as Ø : 1. The value of Ø is approximately 1.618.
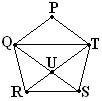
By symmetry PQ//TR and PT//QS Þ PTUQ is a rhombus, in particular PT = QU ¾ 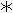
Consider the similar
(Isosceles) Ds, DRUS and DQUT
Then: 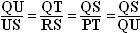 , the last equivalence by
, the last equivalence by 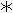 above.
above.
i.e. QU:US = QS : QU and similarly TU : UR
= TR : TU
which establish the lemma.
Lemma 2
A diagonal
of a regular pentagon of side 1 has length Ø .
Let the above ratios be equal to Ø, i.e. QT:RS = Ø : 1.
If RS = 1, then QT = Ø which establishes this lemma.
Proof
proper:
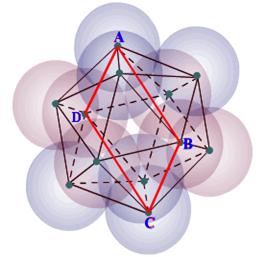
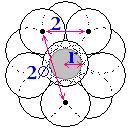
Let the spheres of the icosahedral grouping
have unit radius. (Distinguish between the icosahedron
and the icosahedral-grouping)
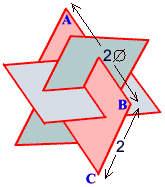
Within the icosahedron
we can identify 3 planes which are mutually perpendicular,
see diagram. Each plane is determined by 2 parallel
edges of the icos. These 2 edges are 2 of the 4 edges
of a rectangle. If the edge length of the icos. is
2 then this rectangle is 2 units wide and 2Ø units long (using Lemma 2).
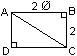 Using
Pythagoras: AC2 = 22 + ( 2Ø )2 = 4 + 4Ø 2 = 4( 1+ Ø 2 )
Using
Pythagoras: AC2 = 22 + ( 2Ø )2 = 4 + 4Ø 2 = 4( 1+ Ø 2 )
Þ AC = 2 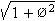
Now the diameter of this
rectangle is the distance from an apex of the icos.
to the opposite apex, i.e. it is the longest diameter
of the icos. So, the radius of the circumscribing
sphere of the icosahedron is
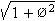 . In the icosahedral-grouping of spheres, this
is the length of a line from the centre of the grouping
to the centre of a ball (or the radius of a sphere
through the centres of the 12 balls),
. In the icosahedral-grouping of spheres, this
is the length of a line from the centre of the grouping
to the centre of a ball (or the radius of a sphere
through the centres of the 12 balls),
Þ Radius R of
circumscribing sphere of the icosahedral-grouping (exosphere) is R = 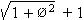 .
.
Similarly, the radius of the sphere that would
fill the space inside the grouping (the endosphere,
say) is
r
= 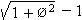
Þ Rr = 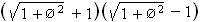 = Ø 2 ¾¾¾
= Ø 2 ¾¾¾ 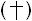
Þ 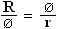
But, (using the rectangle argument) 2 Ø is the diameter of a sphere passing through the points of contact of the
12 spheres, the “contact” sphere, i.e.
Ø is its radius, say R1.
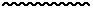 Þ R : R1 = R1 :
r
Þ R : R1 = R1 :
r
i.e. vol. of exo. : vol of contact = vol.
of contact : vol. of endo.
Using
Lemma 1, Ø
2 = 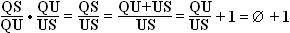
Þ Rr = 1 + Ø, using 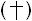 above.
above.
Þ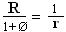 i.e.
i.e. 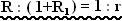
To calculate Ø , note that Ø 2 = Ø + 1, i.e. Ø 2 - Ø - 1 = 0
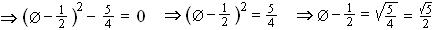
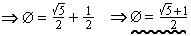
So,
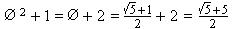
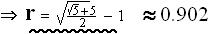
Top view
of the icos. grouping